

김태현
서울대학교 컴퓨터공학부 부교수
김태현
서울대학교 컴퓨터공학부 부교수


전홍기
서울대학교 물리천문학부 대학원생
전홍기
서울대학교 물리천문학부 대학원생
이온트랩을 이용한 양자컴퓨터, 어디까지 왔나?
0. 양자컴퓨터란 무엇인가?
물리학 분야의 가장 흥미로운 사실 중 하나는 세상이 근본적으로 양자역학적이라는 점이다. 우리가 일상생활에서 보는 물체들의 움직임은 근본적으로는 슈뢰딩거 방정식과 힐베르트 공간이라는 양자역학적 개념들로 기술될 수 있으며, F=ma로 대표되는 뉴턴역학은 양자역학의 근사적인 표현일 뿐이다. 원자, 분자보다 훨씬 크기가 큰 시스템에 대해서는 뉴턴역학도 충분히 정확하지만, 물리계의 크기가 작아질수록 부정확 해지며, 결국 양자역학에 의해서만 정확한 예측이 가능해진다. 안타깝게도 양자적 계산은 물리계의 모든 가능한 상태가 중첩되어 존재할 수 있다는 사실 때문에 뉴턴역학적 계산에 비해 급격하게 복잡해진다. 일반적인 컴퓨터를 사용해서는 원자 수십개로 이루어진 시스템의 양자역학적 거동을 계산하는 것도 매우 오랜 시간이 걸리므로 우리는 아직도 단백질과 같은 거대 분자에 대한 정확한 계산을 쉽게 할 수 없다. 세상이 근본적으로 양자역학의 원리를 따라 움직이기 때문에, 단백질이나 DNA와 같은 다체계의 양자이론을 충분한 정확도로 계산하는 것은 미시세계를 정확히 이해하고 활용하고자 한다면 인류로서는 피할 수 없는 문제이다.
양자컴퓨터는 양자비트 또는 큐비트라는 양자적인 성질을 가지는 정보단위를 양자역학의 원리를 이용해 조작하여 계산을 수행하는 기계이다. 본래 양자적으로 작동하므로 앞서 말한 다체계 양자계산을 고전 컴퓨터보다 훨씬 빨리 수행할 수 있으며 [1], 양자 알고리즘의 특성을 이용해 소인수분해, 데이터베이스 검색 등의 양자역학적 계산과는 무관한 응용 분야에서도 고전컴퓨터에 비해 우위를 가지는 경우가 존재한다는 것이 이론적으로 증명되어 있다 [2]. 물론 양자컴퓨터가 모든 업무를 빨리 처리하는 것은 아니어서 사칙연산 등의 간단한 계산은 오히려 고전컴퓨터에 비해 훨씬 느리다. 정리하자면 양자컴퓨터는 정보를 완전히 다른 방식으로 처리하는 기계이며, 양자컴퓨터와 고전컴퓨터는 마치 배와 자동차와 같은 관계라고 볼 수 있겠다. 둘 다 이동수단이지만 완전히 다른 방식으로 작동하고 어떤 상황에서는 배가, 다른 상황에서는 자동차가 더 적합하다. 그러나 자동차로는 절대로 도달할 수 없는, 태평양 한복판의 섬과 같은 문제가 이 세상에는 수 없이 존재하는 것이다.
양자컴퓨터의 성능은 여러 수치로 표시되지만 양자 볼륨이 대표적이다 [3]. 간단히 설명하자면 양자 볼륨은 유용하게 사용할 수 있는 큐비트의 수와 어떤 정확도 이상으로 수행 가능한 양자계산의 길이의 곱이다. 양자컴퓨터로 유용한 계산을 하기위해서는 큐비트 수에 비례하는 많은 양의 정보를 여러 단계를 거쳐 계산해야 하기 때문에 양자 볼륨이 양자 컴퓨터의 성능을 숫자 하나로 나타내는 유용한 지표가 되는 것이다. 이 글에서는 여러가지 양자컴퓨팅 플랫폼 중 하나인 이온트랩을 이용한 양자컴퓨터의 기술수준에 대해 살펴볼 것이다. 양자 볼륨의 구성요소인 큐비트 수와 양자 계산의 정확도에 대해 각각 알아보도록 하자.
물리학 분야의 가장 흥미로운 사실 중 하나는 세상이 근본적으로 양자역학적이라는 점이다. 우리가 일상생활에서 보는 물체들의 움직임은 근본적으로는 슈뢰딩거 방정식과 힐베르트 공간이라는 양자역학적 개념들로 기술될 수 있으며, F=ma로 대표되는 뉴턴역학은 양자역학의 근사적인 표현일 뿐이다. 원자, 분자보다 훨씬 크기가 큰 시스템에 대해서는 뉴턴역학도 충분히 정확하지만, 물리계의 크기가 작아질수록 부정확 해지며, 결국 양자역학에 의해서만 정확한 예측이 가능해진다. 안타깝게도 양자적 계산은 물리계의 모든 가능한 상태가 중첩되어 존재할 수 있다는 사실 때문에 뉴턴역학적 계산에 비해 급격하게 복잡해진다. 일반적인 컴퓨터를 사용해서는 원자 수십개로 이루어진 시스템의 양자역학적 거동을 계산하는 것도 매우 오랜 시간이 걸리므로 우리는 아직도 단백질과 같은 거대 분자에 대한 정확한 계산을 쉽게 할 수 없다. 세상이 근본적으로 양자역학의 원리를 따라 움직이기 때문에, 단백질이나 DNA와 같은 다체계의 양자이론을 충분한 정확도로 계산하는 것은 미시세계를 정확히 이해하고 활용하고자 한다면 인류로서는 피할 수 없는 문제이다.
양자컴퓨터는 양자비트 또는 큐비트라는 양자적인 성질을 가지는 정보단위를 양자역학의 원리를 이용해 조작하여 계산을 수행하는 기계이다. 본래 양자적으로 작동하므로 앞서 말한 다체계 양자계산을 고전 컴퓨터보다 훨씬 빨리 수행할 수 있으며 [1], 양자 알고리즘의 특성을 이용해 소인수분해, 데이터베이스 검색 등의 양자역학적 계산과는 무관한 응용 분야에서도 고전컴퓨터에 비해 우위를 가지는 경우가 존재한다는 것이 이론적으로 증명되어 있다 [2]. 물론 양자컴퓨터가 모든 업무를 빨리 처리하는 것은 아니어서 사칙연산 등의 간단한 계산은 오히려 고전컴퓨터에 비해 훨씬 느리다. 정리하자면 양자컴퓨터는 정보를 완전히 다른 방식으로 처리하는 기계이며, 양자컴퓨터와 고전컴퓨터는 마치 배와 자동차와 같은 관계라고 볼 수 있겠다. 둘 다 이동수단이지만 완전히 다른 방식으로 작동하고 어떤 상황에서는 배가, 다른 상황에서는 자동차가 더 적합하다. 그러나 자동차로는 절대로 도달할 수 없는, 태평양 한복판의 섬과 같은 문제가 이 세상에는 수 없이 존재하는 것이다.
양자컴퓨터의 성능은 여러 수치로 표시되지만 양자 볼륨이 대표적이다 [3]. 간단히 설명하자면 양자 볼륨은 유용하게 사용할 수 있는 큐비트의 수와 어떤 정확도 이상으로 수행 가능한 양자계산의 길이의 곱이다. 양자컴퓨터로 유용한 계산을 하기위해서는 큐비트 수에 비례하는 많은 양의 정보를 여러 단계를 거쳐 계산해야 하기 때문에 양자 볼륨이 양자 컴퓨터의 성능을 숫자 하나로 나타내는 유용한 지표가 되는 것이다. 이 글에서는 여러가지 양자컴퓨팅 플랫폼 중 하나인 이온트랩을 이용한 양자컴퓨터의 기술수준에 대해 살펴볼 것이다. 양자 볼륨의 구성요소인 큐비트 수와 양자 계산의 정확도에 대해 각각 알아보도록 하자.
1. 큐비트 수
현재까지 구현된 대부분의 이온트랩 양자컴퓨터는 양전하를 가지는 이온 큐비트들을 전기장을 이용해 진공에 붙잡아 놓고, 한 방향으로 수 마이크로미터 간격으로 붙여 놓아 “이온 체인”을 만든 것이다. 레이저로 이온의 전자가 가지는 양자 상태를 조작하여 단일 큐비트 연산을 구현하며, 이온들 간의 척력에 의해 생기는 운동모드들을 양자역학적으로 정밀하게 제어해 두 이온 큐비트들 사이의 양자 연산을 구현한다. 양자 연산을 위해서는 각 이온에 레이저 빔을 선택적으로 맞출 수 있어야 하며, 계산에 사용하고자 하는 이온 큐비트와 관련된 운동모드만을 선택할 수도 있어야 하기 때문에 레이저 빔의 형상과 진동수 등에 대한 매우 정확한 조작이 필요하다. 큐비트의 수가 늘어날수록 이온체인의 길이가 길어지고, 운동모드의 수도 늘어나기 때문에 성공적인 연산을 위한 시스템의 요구사항이 급격히 복잡해진다. 이와 같이 큐비트의 수를 늘리는 확장성(scalability)에 대한 연구는 크게 두 방향으로 이루어지고 있다. 먼저 QCCD(quantum charge-coupled device)라는 접근을 살펴보자.
현재까지 구현된 대부분의 이온트랩 양자컴퓨터는 양전하를 가지는 이온 큐비트들을 전기장을 이용해 진공에 붙잡아 놓고, 한 방향으로 수 마이크로미터 간격으로 붙여 놓아 “이온 체인”을 만든 것이다. 레이저로 이온의 전자가 가지는 양자 상태를 조작하여 단일 큐비트 연산을 구현하며, 이온들 간의 척력에 의해 생기는 운동모드들을 양자역학적으로 정밀하게 제어해 두 이온 큐비트들 사이의 양자 연산을 구현한다. 양자 연산을 위해서는 각 이온에 레이저 빔을 선택적으로 맞출 수 있어야 하며, 계산에 사용하고자 하는 이온 큐비트와 관련된 운동모드만을 선택할 수도 있어야 하기 때문에 레이저 빔의 형상과 진동수 등에 대한 매우 정확한 조작이 필요하다. 큐비트의 수가 늘어날수록 이온체인의 길이가 길어지고, 운동모드의 수도 늘어나기 때문에 성공적인 연산을 위한 시스템의 요구사항이 급격히 복잡해진다. 이와 같이 큐비트의 수를 늘리는 확장성(scalability)에 대한 연구는 크게 두 방향으로 이루어지고 있다. 먼저 QCCD(quantum charge-coupled device)라는 접근을 살펴보자.
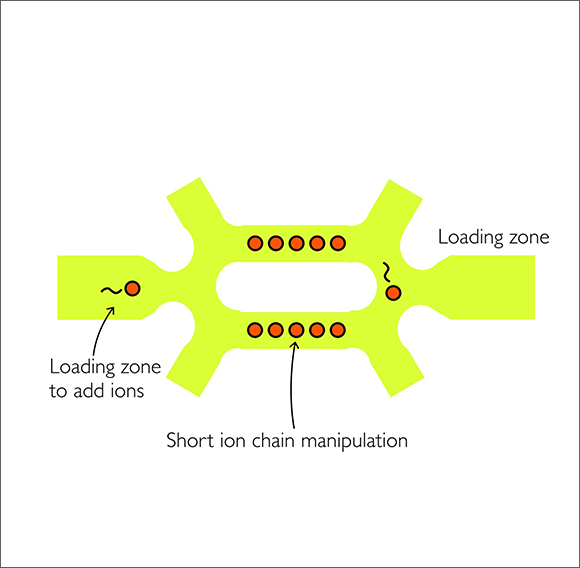
QCCD는 1998년 이온트랩을 이용한 연구로 노벨 물리학상을 받은 미국의 데이비드 와인랜드 (David Wineland)가 제안한 양자컴퓨터의 아키텍처이며, 대전된 입자인 이온을 여기저기로 움직이기 때문에 이미징 장치로 사용되는 CCD의 작동방법을 연상시켜 이와 같은 이름이 붙었다 [1]. 이온 큐비트는 전하를 가지고 있기 때문에 전기장을 사용해 이동시킬 수 있다. 따라서 반도체공정으로 만들어진 미세한 전극들을 이용한다면 이온 큐비트를 “양자 메모리 구역”과 “양자 계산 구역” 사이에서 이동시킬 수 있다. QCCD 방식의 핵심은 양자 알고리즘 수행과정에서 현재 단계에 필요한 큐비트만을 양자 계산 구역으로 불러오고, 나머지 큐비트는 양자정보를 유지한 채 양자 메모리 구역에 놔두는 것이다. 이렇게 하면 큐비트가 실제로 몇 개이던 해당 시점에 양자 게이트를 수행하는데 필요한 큐비트만 따로 떼어 놓기 때문에 앞서 말한 이온 체인의 길이가 길어질수록 시스템의 요구사항이 급격히 늘어나는 문제를 해결할 수 있다. 현재 많은 이온트랩 기반의 회사들이 이런 접근방식을 통해 구현한 양자컴퓨터를 서비스하고 있으며, 특히 최근 미국의 Quantinuum사가 자체 제작한 H1-2 시스템을 이용하여 지금까지 전세계에서 양자 볼륨의 형태로 측정된 값 중에서는 최대값인 4096 (대략 양자 연산 오류가 적은 12개 정도의 큐비트에 해당)을 달성하였다고 발표하기도 하였다 [4]. Quantinuum사는 이후 모델에서 현재의 선형 이온트랩 구조에서 탈피하여, 그리드 형태의 이온트랩을 제작해 다수의 양자 메모리 구역과 양자 계산구역에서 병렬적 양자계산을 수행하려는 로드맵을 밝히기도 하였다 [5].
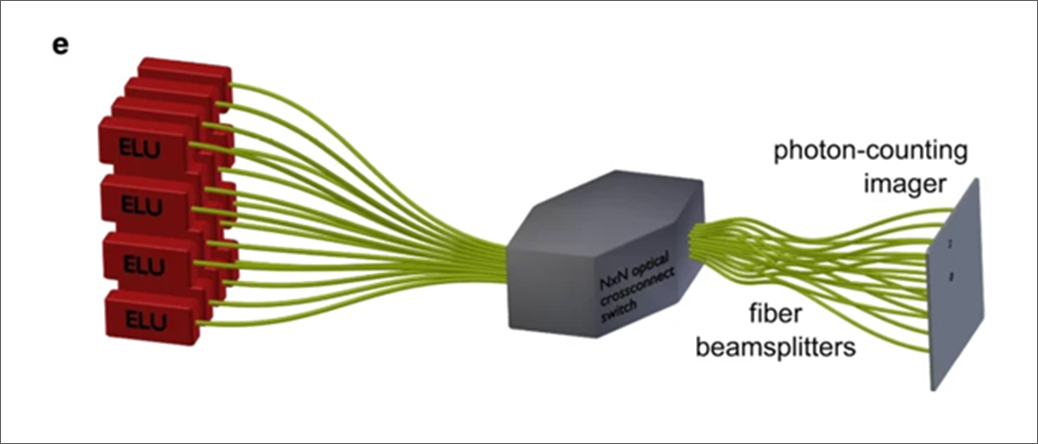
각 ELU(Elementary Logic Unit)에 수십개의 이온 큐비트가 선형 체인으로 존재하며, 광섬유를 통해 통신한다 [7]
이온트랩 양자컴퓨터의 확장성에 대한 두 번째 연구방향은 광자를 이용해 여러 모듈들 사이의 얽힘 상태를 생성하고 이를 활용하여 양자정보를 전송하는 것이다. 광자는 광섬유를 통해 쉽게 이동할 수 있어 확장이 용이하다. 옥스포드 대학교와 듀크 대학교, 그리고 IonQ를 포함한 다양한 이온트랩 기반 양자 컴퓨터 스타트업들에서는 이 방식도 연구하고 있다 [6, 7]. 현재 IonQ는 양자 볼륨 대신 다른 양자 컴퓨팅 업체들과 Quantum Economic Development Consortium (QED-C)라는 산업계 컨소시엄을 구성하고 이를 통해 응용 소프트웨어 기반의 새로운 벤치마킹 패키지를 정의하고 이를 기반으로 IonQ만의 자체적인 양자컴퓨터 성능 지표인 AQ (algorithmic qubit)을 정의하여 20개의 AQ를 달성하였다고 발표하기도 하였다 [8]. 이러한 이온 체인을 기본 모듈로 하여 일종의 양자 네트워크를 구축하는 방식이기 때문에, 성공적으로 구현이 된다면 QCCD방식의 확장성의 한계에 부딪혔을 때 더 많은 큐비트로 확장하기 위한 방법으로 활용될 것으로 예상된다. 대신 광자를 수집할 확률이 낮고 전송과정에서 광자를 손실할 확률은 높아서 충분히 빠른 속도로 모듈 간의 양자 얽힘을 구현하는 것이 어려운 것이 문제로 남아있으며, 이 속도를 늘리는 것이 주요 연구 과제 중 하나이다.
2. 양자 연산의 정확도
양자 연산의 정확도는 고전 컴퓨터보다 양자컴퓨터에서 훨씬 중요한 의미를 가진다. 고전 정보는 쉽게 복제될 수 있기 때문에 오류정정부호를 구현하는 것이 쉬우나, 양자정보는 임의의 양자정보를 복제하는 알고리즘을 만들 수 없다는 “복제 불가능성 정리”(no-cloning theorem) 때문에 오류 정정이 매우 어렵다. 오류 정정이 불가능하지는 않지만 복잡한 양자 계산을 추가적으로 해야만 하며, 따라서 기본적인 게이트 연산들이 상당히 높은 정확도를 가져야 이득을 볼 수 있고 기본 연산이 부정확할 수록 더 많은 추가 큐비트와 연산이 필요하게 된다. 양자 연산은 크게 단일 큐비트 연산과 2-큐비트 연산으로 나눌 수 있으며, 단일 큐비트 연산은 단일 큐비트의 양자 상태를 바꾸는 것을 말하고 2-큐비트 연산은 m번째 큐비트의 상태에 따라 n번째 큐비트의 상태를 조건부로 바꾸는 연산을 말한다. 단일 큐비트 연산은 이온 하나의 큐비트 상태만을 조작하기 때문에 레이저의 조사시간과 진동수만을 정밀하게 조작하면 상당히 높은 정확도로 구현하는 것이 가능하다. 여러 그룹에서 99.99%이상의 단일 큐비트 연산 정확도를 구현하고 있다 [9, 10]. 2-큐비트 연산은 두 큐비트 사이의 정보교환을 위한 통로로 이온의 운동모드를 이용한다. 이온의 운동모드는 노이즈에 취약하고 같은 체인에 더 많은 이온이 있을수록 더 많은 운동모드가 존재하기 때문에 정밀하게 조작하는 것이 쉽지 않다. 예를 들어 10개의 이온 큐비트들로 이루어진 양자 컴퓨터에서 임의의 2개 이온 큐비트들에 2-큐비트 연산을 적용하고자 한다면, 10개의 이온이 특정 운동방향으로 가지는 10개의 운동모드를 양자적으로 완벽하게 조작해야 한다. 약간의 실수라도 있다면 연산 오류가 생기게 된다. 게다가 트랩이나 전자회로의 온도변화, 전압 노이즈 같은 각종 환경적 요인이 이온의 움직임에 영향을 준다. 이온트랩 연구자들은 이온 운동모드의 안정적인 제어를 위해 펄스 성형(pulse shaping)이라는 핵자기공명 (nuclear magnetic resonance)의 아이디어를 참고하여 주변 환경의 변화로 인해 노이즈가 발생하더라도 전체 연산 결과에 영향을 거의 주지 않게 하는 방법으로 성능을 개선하고 있다 [11, 12]. 가장 간단한 방식의 펄스 성형은 핵자기공명의 스핀 에코(spin echo)와 개념적으로 유사하다. 펄스 성형을 통한 2-큐비트 연산의 정확도는 십여 개 수준의 이온 체인에서 99% 정도이며, 이러한 시스템에서 이미 양자 오류정정부호가 구현된 바 있다 [10, 12, 13].
[1] Nature 417, 709–711 (2002)
[2] Nielson, M., Quantum Computation and Quantum Information, Cambridge University Press (2011)
[3] Phys. Rev. A 100, 032328 (2019)
[4] https://www.quantinuum.com/pressrelease/quantinuum-announces-quantum-volume-4096-achievement
[5] https://www.honeywell.com/us/en/news/2020/10/get-to-know-honeywell-s-latest-quantum-computer-system-model-h1
[6] Phys. Rev. Lett. 124, 110501 (2020)
[7] npj Quantum Inf. 2, 16034 (2016)
[8] https://ionq.com/posts/july-25-2022-ionq-aria-part-one-practical-performance
[9] Phys. Rev. Lett. 117, 060504 (2016)
[10] “Quantinuum System Model H1 Product Data Sheet” https://assets.website-files.com/617730fbcf7b7c387194556a/62a8f7244596df4d854c2222_Quantinuum%20H1%20Product%20Data%20Sheet%20v5%2014JUN22.pdf
[11] Phys. Rev. Lett. 120, 020501 (2018)
[12] Phys. Rev. Lett. 112, 190502 (2014)
[13] Nature 598, 281–286 (2021)
양자 연산의 정확도는 고전 컴퓨터보다 양자컴퓨터에서 훨씬 중요한 의미를 가진다. 고전 정보는 쉽게 복제될 수 있기 때문에 오류정정부호를 구현하는 것이 쉬우나, 양자정보는 임의의 양자정보를 복제하는 알고리즘을 만들 수 없다는 “복제 불가능성 정리”(no-cloning theorem) 때문에 오류 정정이 매우 어렵다. 오류 정정이 불가능하지는 않지만 복잡한 양자 계산을 추가적으로 해야만 하며, 따라서 기본적인 게이트 연산들이 상당히 높은 정확도를 가져야 이득을 볼 수 있고 기본 연산이 부정확할 수록 더 많은 추가 큐비트와 연산이 필요하게 된다. 양자 연산은 크게 단일 큐비트 연산과 2-큐비트 연산으로 나눌 수 있으며, 단일 큐비트 연산은 단일 큐비트의 양자 상태를 바꾸는 것을 말하고 2-큐비트 연산은 m번째 큐비트의 상태에 따라 n번째 큐비트의 상태를 조건부로 바꾸는 연산을 말한다. 단일 큐비트 연산은 이온 하나의 큐비트 상태만을 조작하기 때문에 레이저의 조사시간과 진동수만을 정밀하게 조작하면 상당히 높은 정확도로 구현하는 것이 가능하다. 여러 그룹에서 99.99%이상의 단일 큐비트 연산 정확도를 구현하고 있다 [9, 10]. 2-큐비트 연산은 두 큐비트 사이의 정보교환을 위한 통로로 이온의 운동모드를 이용한다. 이온의 운동모드는 노이즈에 취약하고 같은 체인에 더 많은 이온이 있을수록 더 많은 운동모드가 존재하기 때문에 정밀하게 조작하는 것이 쉽지 않다. 예를 들어 10개의 이온 큐비트들로 이루어진 양자 컴퓨터에서 임의의 2개 이온 큐비트들에 2-큐비트 연산을 적용하고자 한다면, 10개의 이온이 특정 운동방향으로 가지는 10개의 운동모드를 양자적으로 완벽하게 조작해야 한다. 약간의 실수라도 있다면 연산 오류가 생기게 된다. 게다가 트랩이나 전자회로의 온도변화, 전압 노이즈 같은 각종 환경적 요인이 이온의 움직임에 영향을 준다. 이온트랩 연구자들은 이온 운동모드의 안정적인 제어를 위해 펄스 성형(pulse shaping)이라는 핵자기공명 (nuclear magnetic resonance)의 아이디어를 참고하여 주변 환경의 변화로 인해 노이즈가 발생하더라도 전체 연산 결과에 영향을 거의 주지 않게 하는 방법으로 성능을 개선하고 있다 [11, 12]. 가장 간단한 방식의 펄스 성형은 핵자기공명의 스핀 에코(spin echo)와 개념적으로 유사하다. 펄스 성형을 통한 2-큐비트 연산의 정확도는 십여 개 수준의 이온 체인에서 99% 정도이며, 이러한 시스템에서 이미 양자 오류정정부호가 구현된 바 있다 [10, 12, 13].
3. 마치며
양자컴퓨터는 우주를 계산하는 가장 자연스러운 방법이지만 동시에 인간이 쉽게 다룰 수 없는 정밀도를 요구하는 상당히 까다로운 기계다. 하지만 지난 수 년간 이온트랩, 초전도체, 중성원자 등의 여러 플랫폼을 사용한 양자 계산 기술이 매우 빠르게 발전해왔다. 컴퓨터 개발 초기에 진공관과 트랜지스터가 경쟁했듯 양자컴퓨터는 여러 방식이 치열하게 경쟁 중이다. 지금 양자 볼륨의 관점에서 지금 가장 우세한 것은 이온트랩 방식이지만 모든 플랫폼이 빠르게 발전하고 있기 때문에, 어떤 시스템이 양자컴퓨터의 애니악이 될지는 미지수이다. 앞으로 수 년간 인류가 어떤 방식으로 대양을 건너 양자계산이라는 신대륙에 도달하게 될 지 흥미를 가지고 지켜보도록 하자.
양자컴퓨터는 우주를 계산하는 가장 자연스러운 방법이지만 동시에 인간이 쉽게 다룰 수 없는 정밀도를 요구하는 상당히 까다로운 기계다. 하지만 지난 수 년간 이온트랩, 초전도체, 중성원자 등의 여러 플랫폼을 사용한 양자 계산 기술이 매우 빠르게 발전해왔다. 컴퓨터 개발 초기에 진공관과 트랜지스터가 경쟁했듯 양자컴퓨터는 여러 방식이 치열하게 경쟁 중이다. 지금 양자 볼륨의 관점에서 지금 가장 우세한 것은 이온트랩 방식이지만 모든 플랫폼이 빠르게 발전하고 있기 때문에, 어떤 시스템이 양자컴퓨터의 애니악이 될지는 미지수이다. 앞으로 수 년간 인류가 어떤 방식으로 대양을 건너 양자계산이라는 신대륙에 도달하게 될 지 흥미를 가지고 지켜보도록 하자.
[참고문헌]
[1] Nature 417, 709–711 (2002)
[2] Nielson, M., Quantum Computation and Quantum Information, Cambridge University Press (2011)
[3] Phys. Rev. A 100, 032328 (2019)
[4] https://www.quantinuum.com/pressrelease/quantinuum-announces-quantum-volume-4096-achievement
[5] https://www.honeywell.com/us/en/news/2020/10/get-to-know-honeywell-s-latest-quantum-computer-system-model-h1
[6] Phys. Rev. Lett. 124, 110501 (2020)
[7] npj Quantum Inf. 2, 16034 (2016)
[8] https://ionq.com/posts/july-25-2022-ionq-aria-part-one-practical-performance
[9] Phys. Rev. Lett. 117, 060504 (2016)
[10] “Quantinuum System Model H1 Product Data Sheet” https://assets.website-files.com/617730fbcf7b7c387194556a/62a8f7244596df4d854c2222_Quantinuum%20H1%20Product%20Data%20Sheet%20v5%2014JUN22.pdf
[11] Phys. Rev. Lett. 120, 020501 (2018)
[12] Phys. Rev. Lett. 112, 190502 (2014)
[13] Nature 598, 281–286 (2021)




