SNU Innovations(vol.07)

Professor Sangbum Kim, from the Department of Materials Science and Engineering, leads the Neuromorphic Materials and Devices Research Lab (NMDL). This laboratory carries out a range of research in neuromorphic computing spanning from semiconductor materials, devices, and artificial intelligence algorithms.

The lexical definition of neuromorphic computing is computing that mimics the brain. However, due to our limited understanding of how the brain operates, perfectly emulating the brain is currently impossible. This has led to a diverse range of approaches in neuromorphic computing research. One such approach involves developing efficient computing methods suited for the currently popular deep learning computations. For example, performing deep learning in an analog rather than digital manner is one method, which is also known as analog in-memory computing (AiMC).

Presently, nearly all computing is done in digital rather than in analog. Depending on the type of operation, there might be advantages to analog computing in terms of circuit area or power consumption. Despite this, the reason for the prevalent use of digital methods is due to the inherent advantages of digital computing. For instance, digital operations can easily handle issues of noise and variation between semiconductor devices and circuits. In a circuit performing operations digitally, if a value of 0.1 is produced, it can be inferred with high probability that the original value was 0. Even in extreme cases where values accidentally change from 0 to 1 or from 1 to 0, errors can be detected and corrected with high reliability using error correction codes. However, in analog operations, it's almost impossible to determine the original value if a noise or error is introduced. Moreover, digital circuits are versatile. For example, a digital circuit designed for multiplication can be flexibly connected to other circuits and memory elements to compute various mathematical functions, which is not as straightforward with analog multipliers. For these reasons, nearly all computing to date has been digital.

However, in deep learning operations, analog circuits can be maximized for their benefits, while their drawbacks are expected to be less problematic. Most of the time and energy in deep learning operations are spent on vector and matrix multiplication (VMM). Depending on the artificial intelligence model, it accounts for up to 90% of the total computation. As seen in the diagram below, VMM operations can be performed very efficiently in analog using resistive device arrays. For instance, if the size of the matrix is 1000 by 1000, the number of multiplications needed for the VMM operation is one million. If there is only one multiplier circuit, it must be used one million times repetitively for one VMM operation, taking a long time. However, if multiple multipliers are made to operate in parallel, the number of repetitions can be reduced. But, because digital multipliers consume a lot of power and occupy a large area, the number of multipliers that can be integrated in a system is limited. On the other hand, the analog multiplier circuit can be much smaller and more power-efficient than its digital counterpart since an analog multiplier can be built with a single resistive device that can perform an analog multiplication operation using Ohm's law. Therefore, a massive number of analog multipliers can be included in a single system, allowing a million multiplications in one VMM operation to be performed at once. In VMM operations, the electrical currents, which are the results of multiplication, are added together by the wires in the array, so no separate adder is needed for analog VMM operations. Additionally, using highly resistive elements and operating at low voltages allows for VMM operations to consume significantly less power than digital methods. These resistive devices serve a similar function to the synapses in our brains and are thus sometimes referred to as synaptic devices.

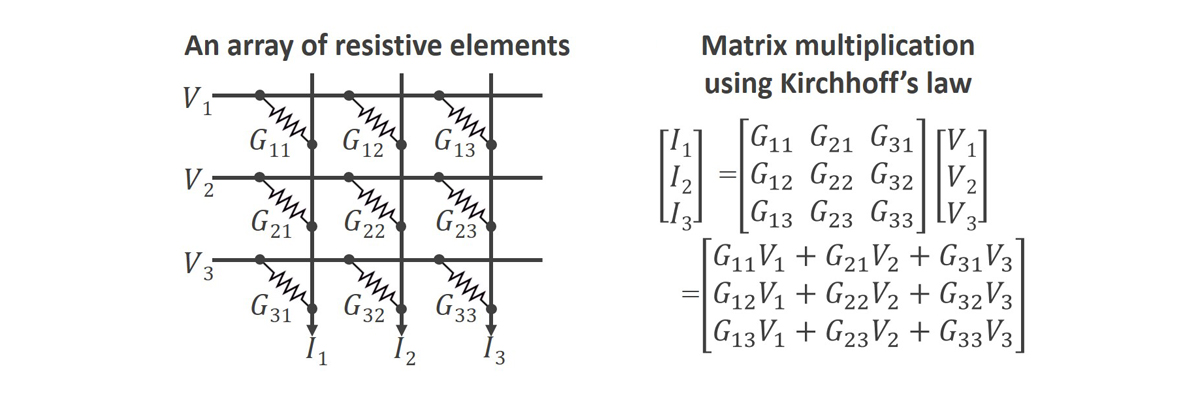
Using these synaptic devices for VMM operations is called in-memory computing or compute in-memory. This is because, in addition to performing multiplications, the synaptic devices also serve a memory function. One of the two multiplication operands is delivered externally in the form of voltage, while the other is stored in the synaptic device itself as resistance value, or more precisely, its reciprocal, the conductance value. For a digital VMM multiplier, all operands must be fetched from external memory. For example, a 1000 by 1000 VMM operation requires fetching more than one million operands. However, a 1000 by 1000 synaptic device array already stores a million operand values, so only a thousand operands corresponding to the input vector need to be fetched for the operation. Typically, fetching operands from memory for digital VMM multipliers consumes a lot of time and energy, a well-known issue called the Von Neumann Bottleneck or memory wall. The recent popularity of high-speed memory products like HBM (High Bandwidth Memory) despite its high price is partly because they can somewhat mitigate this bottleneck. Analog in-memory computing VMM multipliers can drastically reduce the amount of data that needs to be fetched from memory, almost eliminating the Von Neumann Bottleneck. For these reasons, processing VMM operations in analog using a synaptic device array allows for operations to be performed massively in parallel, much faster, and with lower power consumption than its digital counterparts¹.

Despite the efficiency of analog VMM operations, various limitations, such as the reliability issues caused by noise and variation between devices and circuits, still remain in analog computing. Many researchers are conducting studies to find solutions, and the NMDL lab at Seoul National University's Department of Material Science and Engineering is developing solutions from multiple angles. There are broadly three strategies. First is to use existing artificial intelligence algorithms that are not significantly affected by noise in their calculations. For instance, the Restricted Boltzmann Machine (RBM) implements an AI model through stochastic behavior of its neurons. Since stochastic behavior can be implemented by intentionally introducing noise, which requires additional energy and time, the noise inherent in analog operations could improve computational efficiency². The second is to enhance existing AI algorithms to improve their compatibility with analog computing. One solution for addressing variations among devices and circuits is on-chip training, which can self-correct for variations. However, directly applying the deep learning back-propagation algorithm does not work well due to the various non-ideal characteristics of analog devices and circuits. To address this issue, the Tiki-Taka algorithm³, based on the back-propagation algorithm, was proposed, along with new synaptic devices for efficient implementation. Further algorithmic improvements to address remaining issues in these new synaptic devices are also being pursued through device-algorithm co-optimization research⁴.

The third strategy is arguably the most innovative: developing new algorithms suitable for analog in-memory computing. Traditional methods start with an algorithm, designing computing systems and devices to implement a specific algorithm, which are based on digital computing. Thus, when using analog computing systems and devices, mismatches occur, leading to accuracy problems in computation. To overcome these issues, the strategy is to start with the analog system and devise algorithms that fit it perfectly. For example, if we are tackling a problem that can be modeled with various partial diffraction equations (PDE) and one of such PDEs is 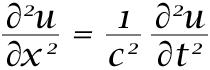, which is the same form as the 1D wave equation, we could solve the given problem by vibrating a string on a guitar the length and density of which are determined based on the parameters used in the PDE. However, because the analog system with the guitar string has non-ideal characteristics such as horizontal motion, finite thickness, and air resistance, it might not solve the PDE and the given problem accurately. We could try to make the ideal guitar string in vain. Alternatively, if we change our perspective and derive an actual PDE that encompasses all the non-ideal characteristics of the analog system with the guitar string. If that PDE can also be used to solve the given problem, we wouldn't necessarily need to correct the issues with the analog system with the string. Based on this philosophy, Joshua Bengio and his colleagues proposed the equilibrium propagation algorithm, which can be applied to end-to-end analog neural network systems⁵. Currently, many researchers including us in NMDL are trying to demonstrate the idea by implementing it with efficient synaptic devices.